- 1. 什么是多任务学习问题
- 2. MTL 的三大技术流派
- 3. 总结
- 4. Reference
做了一段时间的多任务学习在点击率预估中的应用,是时候给多任务学习做个简单的总结了。
1. 什么是多任务学习问题
多任务学习(Multi-Task Learning, MTL)是机器学习的一种范式,本质上属于迁移学习的范畴,但 MTL 与一般大家理解的迁移学习的区别在于 MTL 要借助其它的任务来帮助提升所有任务而非某一个任务的学习效果。另外,MTL 本身也涵盖了多标签学习(Multi-Label Learning)和多分类学习(MultiClass Learning),它们之间的概念从属关系如下图所示:
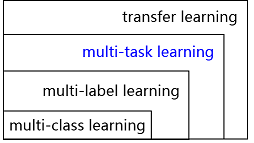
下文中我们讨论的范围只限于 MTL 中的非多标签学习和多分类学习部分,并且这里提到的任务都拥有共同的特征表达空间,每个任务都属于同一种学习类别,即不存在某个任务属于分类任务,而另一个属于回归任务这种情况。
2. MTL 的三大技术流派
MTL 本身是个很古老的概念了,很早就有研究人员开始研究这类问题,按文章 [1] 的分类方法,这些研究结果大体上可以分成 feature-based,parameter-based 和 instance-based 三大流派,下面我们分别简单介绍下各个方法派别的思路。
2.1 基于特征的方法(feature-based methods)
因为这些任务是相关的(至于如何定义这个任务相关性则不是一件容易的事情,有研究人员给出了一些定义和测量方法,但我们这里姑且不求甚解放过这个问题),那么我们有理由假设这些任务一定基于原始特征有一个共同的特征表达。根据如何获取这个共同的特征表达,这一类方法具体又可分为以下两类,一类是基于特征变换(feature transformation),另一类是基于特征选择(feature selection)。
2.1.1 特征变换法(feature transformation approach)
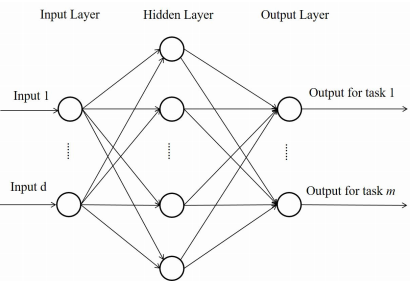
多层前馈神经网络 [3] 就属于这一类方法,这是最早被用于多任务学习的一种方法。下图显示的就是这一种方法的模型结构。
在这个模型中,隐层的输出就可以被看成是所有任务的共同特征表达,也就是原始特征的一个变换。与单任务学习的不同点就在于这个模型的输出是根据任务数决定的,各个输出节点之间是相互独立的。这种网络结构和单任务的网络结构非常相似,改造起来比较简单,这种模型的训练效率也比较高,资源和性能方面都是可以接受的。
多任务特征学习(multi-task feature learning,MTFL) [4]-[5] 和 多任务稀疏编码(multi-task sparse coding,MTSC) [6]则是另一种特征变换的思路,这两种方法都是使用正则化方法来实现的特征变换。具体做法则是先学习到原始特征的线性变换:
\[\hat{x}_j^{i}=U^Tx_j^i,\]其中$x_j^i$表示第$i$个任务的第$j$个特征向量;然后再给出模型输出:
\[f_i(x_j^i)=(a^i)^T\hat{x}_j^i+b_i.\]MTFL 和 MTSC 之间的区别在于,MTFL 中强制矩阵 \(U\) 是正交的,且参数矩阵 \(A=(a^1,...,a^m)\) 是通过 \(l_{2,1}\) 正则达到行稀疏的限制;MTSC 中矩阵 \(U\) 则是过完备的,而且参数矩阵 \(A\) 是通过 \(l_1\) 正则达到稀疏的限制。
这两种方法只能对原始特征做到线性变换,限制了对原始特征的充分学习和表达,方法本身也不太方便扩展。
深度学习方法 相比于前两种方法,深度学习法则采用更为复杂的网络来学习共同的特征表达,然后再在共同特征上各个任务单独学习各自的输出。在深度学习方法中,可以使用诸如 CNN,RNN,FM_EMBEDDING, FFM_BEDDING 等各种最新的技术。这一类方法拥有多层前馈神经网络方法的简单易行,也能使用多种不同 layer 来更好地表达特征。
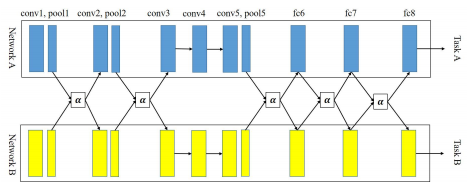
除了这些以外,十字绣网络(cross-stitch network)[7] 是一种很新颖的结构,前面的所有方法中,隐层的参数只有一份,所有任务都是共享同样的隐层,但是十字绣网络可以自动学习到哪些隐层是可以被共享的,以及共享的程度如何。
举个栗子,假设有两个任务$A$和$B$,都使用同样的网络结构,\(x_A^{i,j}(x_B^{i,j})\) 表示第 \(i\) 个隐层的第 \(j\) 个神经元参数,那么对这个参数的十字绣操作就是:
\[\begin{pmatrix} \hat{x}_A^{i,j}\\\hat{x}_B^{i,j} \end{pmatrix}=\begin{pmatrix} \alpha_{AA}&\alpha_{AB}\\\alpha_{BA}&\alpha_{BB} \end{pmatrix} \begin{pmatrix} x_A^{i,j}\\x_B^{i,j} \end{pmatrix}\]\(\hat{x}_A^{i,j}(\hat{x}_B^{i,j})\) 则是 \(A\) 和 \(B\) 各自网络联合学习到的新的隐层参数,\(\alpha_{XX}\) 是可学习的参数,如果参数 \(\alpha_{AB}\) 和 \(\alpha_{BA}\) 接近于0,则意味着这两个任务没什么关系,这两个网络等价是独立各自学习的。但十字绣网络为此付出的代价是每个任务需要有个网络外,还需要更多的联合参数,这样使得学习的效率和性能大打折扣。
2.1.2 特征选择法(feature selection approach)
获取不同任务的共同特征表达,特征选择法的思路则是从原始特征中选出一个子集作为共同特征。选择的办法也大体分为两类:
第一类基于对参数矩阵 \(W=(w_1,...,w_m)\) 的正则化约束,对于任务 \(i\):
\[f_i(x)=(w^i)^Tx+b_i\]则是学到的线性变换,使用最广的正则化方法是 \(l_{p,q}\) 范数。第二类则是利用参数矩阵 \(W\) 的稀疏概率先验。
这两类方法本文就不具体展开说明了,原因是特征选择方法从本质上来看是属于特征变换方法的一种特例,只是变换矩阵只由 {0,1} 组成而已,且通常情况下,特征变换方法要好于特征选择方法。
2.2 基于参数的方法(parameter-based methods)
基于参数的方法是使用模型参数来关联不同的任务,根据关联方式的不同,大概可以分为以下 4 类。
2.2.1 低秩法(low-rank approach)
相似的学习任务往往意味着模型的参数 \(w_i, i=1,...,m\) 是相似的,那也就意味着参数矩阵 \(W=(w_1,...,w_m)\) 是低秩的。因此可以假设不同任务的参数共享一个低秩子空间且有形式 [8]:
\[w^i=u^i+\Theta^Tv^i\]这里的 \(\Theta\in R^{h\times d},\,h< d\) 是共享的低秩子空间。然后基于此再构造目标函数进行求解,在构造目标函数的时候大家就各显神通了,产生了一堆方法,比如一个常见的技巧是加入\(W\) 的迹范数(trace norm)作为正则化项,因为迹范数可以限制矩阵成为低秩的。
这一类方法倒是挺有趣的,只是参数量会大非常多,因为这个 \(\Theta\in R^{h\times d},\,h< d\) 矩阵,以及每个任务独有的参数 \(u^i,\,v^i\) 都是需要学习的。更重要的是,这类方法似乎只能用于线性模型,当扩展到非线性的时候会导致发散。
2.2.2 任务聚类法(task clustering approach)
任务聚类法则是将各种任务做个分类,同一类的任务共享完全相同或者相似的模型参数。最早的方式是两阶段的,即先分类再学习 [9],显然这种方式效果不会太好,所以后续的这类方法都是分类和参数同时学的。其实这类方法和低秩法是相关的,聚类法可以看成是一种特殊的低秩法,比如有 \(r< m\) 个聚类,每个类使用一个模型,那么参数矩阵 \(W\) 就至多是秩为 \(r\) 的。但是这类方法过于独特,不太方便扩展,而且最大的问题是任务聚类往往只能捕捉同一个类别任务的正相关性,而忽略了不同类别任务的负相关性。
2.2.3 任务关系学习法(task relation learning approach)
这类方法通过给定一些先验知识,然后设计巧妙的损失函数,从数据中学习任务之间的关系,让关系比较近的任务的模型具有相同或者相似的参数。其中的关系度量可以用各种办法,比如任务相似度(similarity),任务相关性(correlation),任务协方差(covariance)等等。这类方法的缺点也很明显,就是需要设计的非常精巧,因此扩展性就不好。
2.2.4 分解法(decomposition approach)
分解法假设参数矩阵 \(W=(w_1,...,w_m)\) 可以被分解为 2 个或多个部分,即:
\[W=\sum_{k=1}^hW_k,\]这类方法中大部分的目标函数都可以写成如下的形式:
\[min\,\, L(W,b)+\sum_{k=1}^hg(W_k)\]举个简单的栗子 [10] 来说明这个方法的思路,假设 \(h=2\),\(g_1(\cdot)\) 和 \(g_2(\cdot)\) 定义为:
\[g_1(W_1)=\lambda_1||W_1||_{\infty,1},\,g_2(W_2)=\lambda_2||W_2||_{1},\]其中 \(\lambda_1\) 和 \(\lambda_2\) 是正则化系数,\(g_1(W_1)\) 可以使得 \(W_1\) 是行稀疏的,因此可以帮助挑选出最重要的特征,\(g_2(W_2)\) 可以使得 \(W_2\) 是 \(L1\) 稀疏的。所以综合起来看,当对应行在 \(W_1\) 和 \(W_2\) 中都稀疏时,\(W\) 可以去掉对所有任务都不重要的特征,同时,\(W_2\) 又可以帮助挑出对某一个任务很重要但对其它任务不重要的特征。这类分解法中,分解的个数 \(h\) 是个非常重要的参数,往往需要人凭经验判定,这也算是这类方法的一大缺陷。
2.3 基于实例的方法(instance-based methods)
这是个冷门的流派,基本上没有什么人在这个方法上灌水,除了文章 [2]。这套方法的思路是先估计样本来自自身任务的概率与来自其它任务的概率比值,再用这个比值计算该样本的权重,最后使用加权的样本用于学习每一个任务的模型。
3. 总结
如果说要求训练效率高,并且模型可扩展性强,效果也要好,基于这些需求,在调研了很多算法以及尝试了很多模型后,2.1.1 特征变换法中的深度学习方法是一个比较理想的选择。
但是,基于特征的方法有一个很大的问题,由于权重是共享的,当这些任务中存在不那么相关的任务时,任务之间会相互扰乱,影响效果。另外,以上综述的这些令人眼花缭乱的方法并非孤立的,在很大程度上可以结合起来使用,这里有着巨大的优化空间,尤其是部分任务的相关性没那么强的时候,比如可以对相关性不强的任务的最后输出网络做差异化处理,确保每个任务都能达到最佳的训练效果。
4. Reference
[1] Yu Zhang & Qiang Yang, “A survey on multi-task learning”, arXiv, 2018
[2] S. Bickel, J. Bogojeska, T. Lengauer, and T. Scheffer, “Multi-task learning for HIV therapy screening,” in ICML, 2008.
[3] R. Caruana, “Multitask learning,” MLJ, vol. 28, no. 1, pp. 41–75, 1997.
[4] A. Argyriou, T. Evgeniou, and M. Pontil, “Multi-task feature learning,” in NIPS, 2006.
[5] A. Argyriou, T. Evgeniou, and M. Pontil, “Convex multi-task feature learning,” MLJ, vol. 73, no. 3, pp. 243–272, 2008.
[6] A. Maurer, M. Pontil, and B. Romera-Paredes, “Sparse coding for multitask and transfer learning,” in ICML, 2013.
[7] I. Misra, A. Shrivastava, A. Gupta, and M. Hebert, “Cross-stitch networks for multi-task learning,” in CVPR, 2016.
[8] R. K. Ando and T. Zhang, “A framework for learning predictive structures from multiple tasks and unlabeled data,” JMLR, vol. 6, pp. 1817–1853, 2005.
[9] S. Thrun and J. O’Sullivan, “Discovering structure in multiple learning tasks: The TC algorithm,” in ICML, 1996.
[10] A. Jalali, P. Ravikumar, S. Sanghavi, and C. Ruan, “A dirty model for multi-task learning,” in NIPS, 2010.