1. 定义
\[\begin{equation} \Psi(x) = \frac{\mathrm{d}}{\mathrm{d}x}\ln\Gamma(x)=\frac{\Gamma'(x)}{\Gamma(x)}. \end{equation}\]这是第一个 多伽马函数。
2. 性质
双伽马函数的数值通常通过查表的方式进行,但是在程序中查表并不是一个好方法,如果能直接计算则更好。计算双伽马函数的值主要利用了它的以下性质:
(1) 递推关系
\[\begin{equation}\tag{1} \Psi(x+1)=\Psi(x)+\frac{1}{x}. \end{equation}\](2) 反射公式
\[\begin{equation}\tag{2} \Psi(1-x)=\Psi(x)+\pi \cot(\pi x). \end{equation}\]由上面的公式 (1) 和公式 (2) 可以得到:
\[\begin{equation}\tag{3} \Psi(-x)=\Psi(x)+\pi \cot(\pi x)+\frac{1}{x}. \end{equation}\](3) 特殊值
\[\begin{equation}\tag{4} \Psi(1)=-\gamma. \end{equation}\]其中,\(\gamma\) 是欧拉-马斯刻若尼常数,它的近似值为 \(\gamma=0.5772156649015328606065\)。
(4) 近似公式
同时,当 \(x\) 在 \((0,1)\) 区间内时,可以使用下面的近似公式计算:
\[\begin{eqnarray*} \Psi(x)=&-&0.515095835950807-0.000014382050162/x^3+0.000557958765350/x^2\\ &-&1.008336779674558/x+1.389927456533864x\\ &-&0.586786525683560x^2+0.142984009331572x^3 \end{eqnarray*}\]上面的近似公式是通过数据拟合出来的一个公式,一般来说结果可以精确到小数点后 6 位。拟合的原始数据采集来源于用初等函数表示的 \(\Psi(x)\) 的值,其中 \(0<x<1\)。
3. 算法
根据上文列出的性质,计算双伽马函数值的算法如下 (此算法来自这里)
-
如果 \(x\) 为负数,则使用 (3) 式进行计算
-
如果 \(x=1\),则返回 -0.57721566490153286
-
如果 \(x>1\),则使用 (1) 式进行降阶计算
-
如果 \(0<x<1\),则使用上文列出的近似公式进行计算
4. 代码
函数格式:\(double \, \mathrm{digamma}(double \, x)\)
例子:
\[\begin{eqnarray*} \mathrm{digamma}(12.345678) &=& 2.47221806261\\ \mathrm{digamma}(0.123456789)&=&-8.49073788439\\ \mathrm{digamma}(-0.7654321) &=&-3.20283490078\\ \mathrm{digamma}(0.5) &=&-1.96351251863 \end{eqnarray*}\]函数曲线:
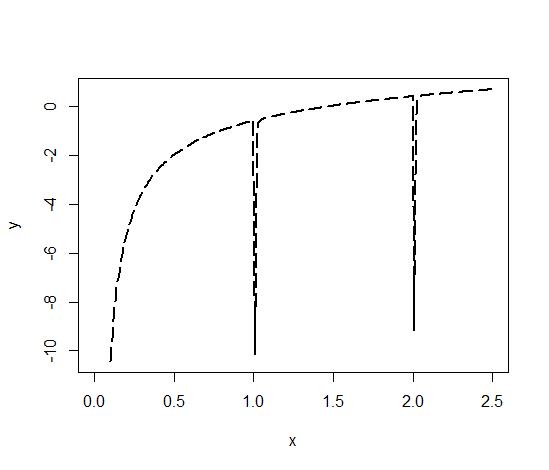
问题:
下面的代码是通过递归实现的,由于不是尾递归,递归的深度有限,如果 \(x\) 的值很大,比如超过 1000,则非常耗内存资源。这时可以将 \(x>1\) 的那段单独拿出来,写成尾递归的形式,则可以支持 \(x\) 很大的计算。
源代码:
#!/usr/bin/python
# -*- coding: UTF-8 -*-
'''
Created on 2016-07-23
@author: jamescao(caoxiaoqing)
'''
import math
def digamma(x):
if( abs(x-1)<1e-8 ):
return -0.57721566490153286
if( abs(x)<1e-8 ):
return None
if( x<0 ):
return digamma(-x)+math.pi/math.tan(-math.pi*x)-1/x
elif( x>1 ):
return digamma(x-1)+1/(x-1)
else:
return -0.515095835950807-0.000014382050162/(x*x*x)\
+0.000557958765350/(x*x)-1.008336779674558/x\
+1.389927456533864*x-0.586786525683560*(x*x)\
+0.142984009331572*(x*x*x)